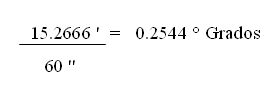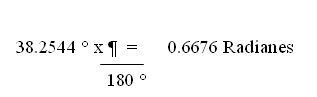Ley de seno
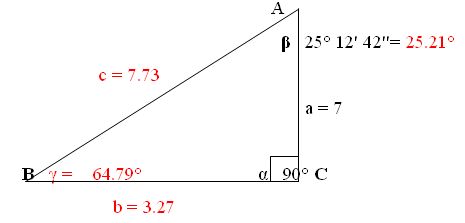
La ley de seno es una relación de tres igualdades que siempre se cumplen entre los lados y ángulos de un triángulo cualquiera. En ocasiones necesitarás resolver ejercicios que envuelven triángulos que no son rectángulos. La ley del Seno y la del coseno son muy convenientes para resolver problemas de triángulos en los que no hay ningún ángulo rectángulo como los discutidos en la sección de trigonometría básica.Veamos el siguiente triángulo:

Entonces

La ley del seno nos dice que la razón entre la longitud de cada lado y el seno del ángulo opuesto a el en todo triángulo es constante.
La ley del seno se escribirá como sigue:

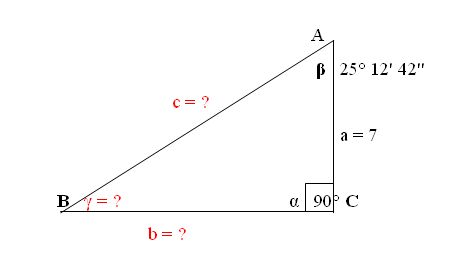
 2.Conociendo β, podemos conocer γ, ya que α = 90°, así:
2.Conociendo β, podemos conocer γ, ya que α = 90°, así:








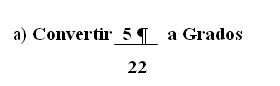
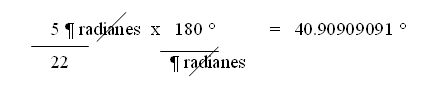
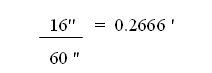 Ahora sumamos los 0.2666 minutos con los 15 minutos que ya se tienen,
Ahora sumamos los 0.2666 minutos con los 15 minutos que ya se tienen,